triangle1.net

This first entry may be regarded as more philosophically orientated, it covers topics such as vagueness, a philosophical construct central to fuzzy set theory.  To understand the concept behind fuzzy sets, it is of importance to understand the concept of vagueness in a broader sense. Vagueness in philosophy is an intriguing and broadly covered topic, and perhaps may be best described by examining Sorites Paradox. This paradox is named after the vague object of which it is concerned, namely a heap (sorites being Greek word for heap).

The paradox has two premises: When standing next to a 4 meter large pile of sand for example, the object is considered a heap; this may be seen as the first premise. The second premise is that, if we would remove one grain of sand from the heap, the object may still be considered a heap.

The paradox may be found in the iteration of the second premise and possible conclusion. After repeating the second premise, if enough grains of sand are removed, only one grain will remain. According to the two premises, one might argue that one grain should still be considered a heap. And if not, when did it change from being a heap to not being a heap? The answer to this paradox has proven to be difficult to find with classic logic.

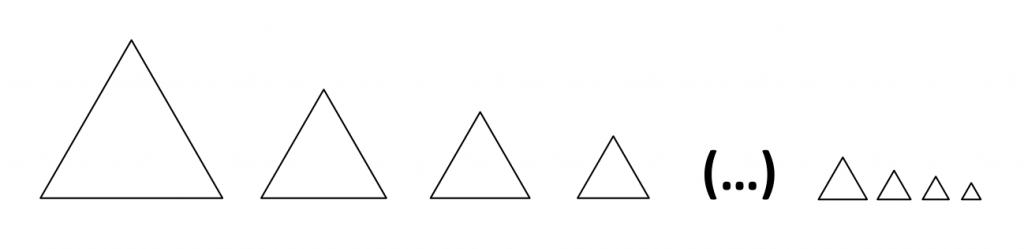
Moving from the philosophical domain, the idea of vagueness and relationship to classical set theory has been described since the early 1930’s. Most notably by Black (1937) and Hempel (1939), who were one of the first scholars to describe the notion of vagueness and the discrepancies it caused when applied to classical sets. These shortcomings of traditional logic have also been acknowledged by Russell (1923, pdf);

All traditional logic habitually assumes that precise symbols are being exployed. It is therefore not applicable to this terrestrial life, but only to an imagined celestial existence.

One of the most convincing examples to show the shortcomings of traditional logic, is the application of classical negations to vague concepts. A natural reaction to the paradox would be to argue that the second premise is false. If one of the premises is false, the conclusion would also be incorrect. However, according to classic logic, this implies that with the rejection of this premise, the negation is accepted. This may also be considered unacceptable since at some point in time, the removal of a single grain would in fact lead to the entity not being considered a heap anymore.

Both Black and Hempel, mainly focused on the effects of vagueness in natural language Rolf (1980), and the implications from a philosophical point of view (such as the issues described above). Although these are classical works and may be considered groundbreaking, due to their philosophical nature, these concepts found no applications in other fields of science.

It is worth to note that the example used here, is entirely focused on linguistic vagueness (in much of the same fashion as Black and Hempel’s works). There are some scholars however, that dismiss the notion that all vagueness is of a linguistic nature, and propose the idea of vague objects such as Van Inwagen (1990). Others even consider vague instrumental music as a proof that vagueness is not only bound to linguistics (Sorensen, 2011). This however, may be seen as a pure philosophical discussion that does not influence the logic behind the concepts of fuzzy set theory.

I believe it is very interesting to see vagueness and unpredictability as constructs embedded in our universe. In fact one may argue that Heisenberg’s uncertainty principle is actually proof that vagueness exists, even at quantum scale.

I have been playing with the idea  of writing a short introduction to fuzzy set theory for a while now. Today I finally had time to start writing the first entry to this series, an introduction to vagueness. The posts will be mainly adaptations and excerpts from my thesis and other articles I’ve written, if you’re interested in learning the basics and philosophy that define fuzzy set theory I hope this is a good starting point. Also I hope it will generate some exposure for fuzzy set theory in general (looking at visitor counts of this website I doubt it but you never know).

The first time I came in to contact with fuzzy sets was during my Bachelor’s degree in Electrical Engineering. As part of the curriculum of a Control Systems course it was decided to add one class on fuzzy control systems. This however was way too brief  for me to develop a good understanding or to spark some interest in this subject in the first place. I just couldn’t understand why it would make sense to introduce constructs like fuzziness into the “perfect” world of mathematics where everything is crisp, sound and nicely structured (this is what every mathematician or engineer likes right).

This view changed during my Master’s degree when I had the honor to have my thesis supervised by Uzay Kaymak and Rui de Almeida at the Eindhoven University of Technology, both experts in fuzzy set theory. Their passion and knowledge on the subject inspired me to specialize in fuzzy sets. For me it helped to understand the broader philosophical concepts first before looking at fuzzy sets itself (it helps to put things in perspective I think) . That is why this series will start with a short philosophical review of fuzziness and vagueness in the broadest sense. After this I will touch upon the mathematics behind fuzzy set theory and fuzzy logic. This will be followed by a brief introduction on  evolving fuzzy Takagi-Sugeno algorithms, the implementation I’ve written in R is based on this theorem.